A. MATRIX STRUCTURE AND NOTATION
1) A matrix is a rectangular arrangement of numbers. The matrix is usually denoted by a capital letter.
A
= ![]() D
=
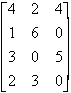
D
= 
2) The dimensions of a matrix are given by the number of rows and columns in the matrix (i.e. the dimensions are r by c). For the matrices above,
A is 2 by 2
D is 4 by 3
3) The individual elements of a matrix can be referred to by specifying the row and column in which it occurs. Lower case numbers are used to represent individual elements, and should match the upper case letter used to denote matrix. For example, individual elements from matrices A and D above can be referred to as,
a11 = 1
a21 = 7
d22 = 6
d12 = 2
B. TYPES OF MATRICES
1) Square matrix - the number of rows and columns are equal. Matrix A above is a square matrix (2 by 2), matrix D is not (4 by 3). A symmetric matrix is an important variation of the square matrix. In a symmetric matrix, the value in position “ij" equals the value in position “ji" (where i ¹ j). For example, if c31 = 5 then c13 is also 5.
2) Scalar - a single number can be thought of as a 1 by 1 matrix and is called a scalar.
3) Vector - a single column or single row of numbers is called a vector. The dimensions of a row vector are (1 by c), where "c" is the number of columns, and the dimensions of a column vector (r by 1), where "r" is the number of rows.
4) Identity matrix - this special square matrix consists of all ones on the main diagonal, or principal diagonal, and zeros in all the off diagonal positions. The following are examples of identity matrices,
E =  F =
F = 
The diagonal matrix is a generalization of the identity matrix. A diagonal matrix can have any value on the main diagonal, but also has zeros in the off diagonal positions.
C. MATRIX TRANSPOSE
The transpose of a matrix consists of a new matrix such that the rows of the original matrix become the columns of the transpose matrix. The transpose matrix is denoted with the same letter as the original matrix followed by a prime (e.g. the transpose of X is X).
D
=  D =
D = 
D. MATRIX ADDITION AND SUBTRACTION
Matrices to be added or subtracted must be of the same dimensions. Each element of the first matrix, (a) is added (or subtracted) from the corresponding element of the second matrix, (b).
A
= 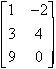 B =
B = 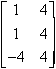 A+B =
A+B = 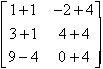 =
=
![]()
E. MATRIX MULTIPLICATION
Multiplication by a scalar - in this type of multiplication each element of the matrix is simply multiplied, element by element, by the scalar value.
A
=  B =
[7] A *
B
= 7 *
B =
[7] A *
B
= 7 *  =
=

Element by element multiplication - matrix multiplication is not usually done by matching each i,jth element of one matrix with the corresponding ijth element of the second matrix. This is called elementwise multiplication and it is not the normal mode of matrix multiplication and should not be used unless specifically requested.
The standard method of matrix multiplication requires that the number of columns in the first matrix equal the number of rows in the second matrix. If the first matrix is (r by c) and the second is (r by c), in order to multiply the matrices, c must equal r. The resulting matrix will have the dimensions (r by c).
Multiplication is accomplished by summing the cross products of each row of the first matrix and each column of the second matrix.
A =  X =
X = ![]()
Since A is 3 rows by 2 columns, and X is 2 by 2, then the columns of the first matrix equals the rows of the second matrix, and the matrices may be multiplied.
A*X =  *
*
![]() =
=
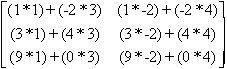 =
=

the new dimensions for the product of A * X are,
|
|
|
¯ |
must be equal |
¯ |
|
|
|
(3 |
x |
2) |
x |
(2 |
x |
3) |
|
|
|
|
new dimensions |
|
|
|
Note that though we can multiply A * X, we could not have done the multiplication the other way (i.e. X * A), since the dimensions would not have matched. That is, we could pre-multiply by A, but could not pre-multiply by X.
F. SIMPLE MATRIX INVERSION (2 by 2 matrix only)
Matrices are not “divided", but may be inverted. Instead of “dividing" A by B, one would multiply A by the inverse of B. The inverse of a (2 by 2) matrix is given by,
A =![]() A–1 =
A–1 =
![]()
The scalar value resulting from the calculation “(a%d) – (b%c)" is called the determinant. The matrix cannot be inverted unless the inverse of the determinant exists (is defined). It will not exist in a case such as the one below since (1+0) is not defined.
A =![]() A–1 =
A–1 =
![]()
This occurs in regression when two variables are linearly related.
An example of the inversion of a 2 * 2 matrix is given below.
B =![]() B–1 =
B–1 =
![]()
Note that a matrix times its inverse (i.e. B % B–1) results in an identity matrix. By definition, the inverse of a matrix G is a matrix which when multiplied by G produces an identity matrix, or G%G–1=I.
G. SIMPLE LINEAR REGRESSION
Solving a simple linear regression with matrices requires the same values used for an algebraic solution from summation notation formulas. These are;
n
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
where n is the size of the sample of data. To obtain these values in the matrix form we start with the matrix equivalent of the individual values of X and Y, the raw data matrices.
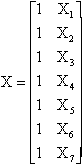
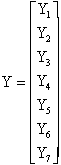
The column of ones is necessary, and represents the intercept. Omitting this column would force the regression through the origin. The next step in the calculations is to obtain the X¢X, X¢Y and Y¢Y matrices. These calculations provide the sums of squares and cross products.
 =
=

 =
=
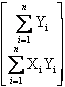

The regression coefficients, b0 and b1, are then given by, B = (X¢X)–1X¢Y, where
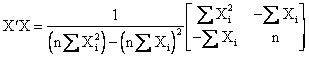
and since
![]()
where Sxx is the corrected sum of squares of X.
Then

and the regression coefficients can be obtained by,
 =
=

=
 =
=
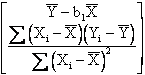 =
=
 =
=
![]()
The remaining calculations usually needed to complete the compliment of calculations for the simple linear regression is the sum of squared deviations or error term. The matrix formula is
SSE = Y¢Y – B¢X¢Y = SY2 –
[b0 b1]![]()
= SY2 – (b0*SY + b1*SXY) = UCSSTotal – UCSSReg
These calculations produce the same algebraic equations for b0, b1, and SSE that are given in most statistics texts. The advantage of using the matrix version of the formulas is that the matrix equations given above will work equally well for multiple regression with two or more independent variables.
The ANOVA table calculated with matrix formulas is
|
|
Uncorrected |
|
Corrected |
|
|
Source |
d.f. |
Sum of Squares |
d.f. |
Sum of Squares |
|
Regression |
2 |
B¢X¢Y |
1 |
B¢X¢Y – CF |
|
Error |
n–2 |
Y¢Y–B¢X¢Y |
n–2 |
Y¢Y – B¢X¢Y |
|
Total |
n |
Y¢Y |
n–1 |
Y¢Y – CF |
where the
correction factor is calculated as usual,
![]() .
.
The value for R2 is calculated as
![]() ,
and is often expressed as a percent. Note that this
calculation employs corrected sums of squares for both SSRegression and
SSTotal.
,
and is often expressed as a percent. Note that this
calculation employs corrected sums of squares for both SSRegression and
SSTotal.
The Mean Squares (MS) for the SSRegression and SSError are calculated by dividing the SS (corrected sum of squares) by their d.f. (degrees of freedom). The test of hypotheses for [H0:= b1] is then calculated as;
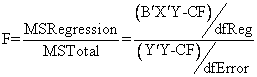
or
![]()
where
![]() is
obtained from the
VARIANCE COVARIANCE matrix.
is
obtained from the
VARIANCE COVARIANCE matrix.
The VARIANCE COVARIANCE matrix is calculated as from the (X¢X)–1 matrix.
![]()
where the cij values are called Gaussian multipliers. The VARIANCE-COVARIANCE matrix is then calculated from this matrix by multiplying by the MSError.
![]()
The individual values then provide the variances and covariances such that
MSE*c00 = Variance of b0 = VAR(b0)
MSE*c11 =
Variance of b1 = VAR(b1), so
![]()
MSE*c01 = MSE*c10 = Covariance of b0 and b0\1 = COV(b0,b1)
It is important to note that the variances and covariances calculated from the (X¢X)–1 are for the bi (bi estimates), not for the Xi values. Also, COV(b0,b1) ¹ COV(X0,X1).



 X¢Y=
X¢Y=
 Y¢Y=
[103075]
Y¢Y=
[103075] 




